12 LAWS AND RULE OF BOOLEAN ALGEBRA

basic rules of boolean algebra

BOOLEAN ALGEBRA'S RULES AND LAWS:

  A English mathematician, philosopher and logician George Boole 1854 given a mathematical theories and few logical algebra named as Boolean Algebra..which consist of 12 laws or rule which briefly described Boolean Algebra which are:

            

1.    A + 0 = A

2.    A + 1 = 1

3.    A . 0  = 0

4.    A . 1  = A

5.    A + A = A

6.    A + Ā = 1

7.    A . A = A

8.    A . Ā= 0

9.    ﬢ(ﬢA) = A

10. A + A B = A

11. A + ĀB = A + B

12. (A + B)(A + C) = A + BC

Derivation of Laws Using Gates And Truth Table:

RULE # 1 (  A + 0 = A) 

A + 0 = A

A	0	A+0
0	0	0
1	0	1

RULE # 2 (A + 1 = 1)

A + 1 = 1

A	1	A+1
0	1	1
1	1	1

RULE # 3 (  A . 0  = 0)

A .0 =0

A	0	A . 0
0	0	0
1	0	0

RULE# 4 (A . 1  = A)

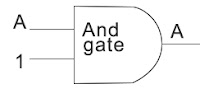A. 1= A

A	1	A . 0
0	1	A
1	1	A

RULE #5 ( A + A = A)

A + A = A.

A	A	A +A
0	0	A
1	1	A

RULE # 6(A + Ā = 1)

A + Ā = 1

A	Ā	A+ Ā=1
0	1	1
1	0	1

RULE # 7(A . A = A)

A.A=A

A	A	A .A
0	0	A
1	1	A

RULE # 8 (  A . Ā= 0)

A . Ā= 0

A	Ā	A . Ā
0	1	0
1	0	0

RULE # 9 (ﬢ(ﬢA) = A)

A Double not = A

RULE #10 ( A + A B = A)

= A+ AB

= A (1 + B)

= A (1)             (from rule no 2 A + 1= 1, replace the variable A by B so  B+1 or 1+B=1)

= A

A + AB = A

RULE # 11( A + ĀB = A + B)

= A + ĀB

= A + AB + ĀB   (from rule no 10,A+AB=A)

= A + B(A +Ā )

= A + B(1)          (from rule no 6, A +Ā = 1)

= A + B              (which is equal to right hand side)

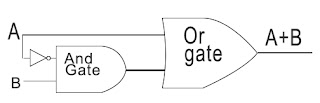 A + ĀB = A + B

RULE#12(. (A + B)(A + C) = A + BC)

= (A + B)(A + C)

= AA + AC + AB + BC

= A + AC + AB + BC        (from rule no 7 A.A = A)

= A(1 + C) + AB + BC

= A (1) + AB +BC             (from rule no 2, 1+C=1)

= A + AB + BC

= A + BC                           (from rule no 10 , A + AB = A) hence it is equal to right hand side

(A+B)(A+C)=A+AB

                                           physics label